“Se es ingeniero mientras se participa en la elaboración de un reglamento o cuando se diseña una estructura no cubierta por ningún reglamento o en los momentos en que se decide si se va a aplicar una norma reglamentaria o ninguna y si sí, cuál; se deja de ser ingeniero se deja de ser profesionista –para convertirse en técnico- en la medida que se deja de pensar críticamente y se aplican recetas, reglas, normas elaboradas por otros. No es humanamente posible, ni físicamente posible diseñar una estructura con certeza absoluta de que jamás ingrese a un estado límite. Nos incumbe en cambio como ingenieros, como profesionales responsables ante el cliente y ante la sociedad, hacer las cosas lo mejor que podamos: imprimir a las estructuras que diseñamos las probabilidades óptimas de ingreso a estados límite.”

Emilio Rosenblueth*

Resumen

La normatividad actual de diseño de puentes en México incluye un capítulo para el diseño ante acciones del viento sobre estas estructuras. En ese capítulo se presentan mapas de contorno de velocidades de viento que sirven para evaluar la presión de viento para diseño, que se emplea junto con un factor de carga, posiblemente obtenido a partir del factor de carga recomendado en el reglamento estadounidense, sin embargo no existe un reporte detallado de la calibración de este factor para las condiciones mexicanas. En este artículo se presenta una reseña de un trabajo previo donde se proponen disposiciones de diseño, y se efectúo un trabajo de calibración, para diseñar puentes en México para un nivel de confiabilidad preestablecido. El objetivo principal de este estudio es emplear la propuesta de diseño desarrollada anteriormente y realizar un ejemplo de aplicación para un puente determinado, comparando la propuesta de diseño, con la normatividad de SCT, así como con el reglamento estadounidense y el canadiense.

1.-INTRODUCCIÓN

Las cargas de viento que actúan sobre los puentes se pueden representar con las fuerzas estáticas, fluctuantes, y de auto-excitación aeroelástica que se obtienen de promedios para cierto intervalo de tiempo. La mayoría de códigos de diseño de puentes (SCT, 2001; CAN/CSA-S6-06, 2006; AASHTO, 2007) adoptan el método de factor de ráfaga, aunque los formatos y expresiones difieren para los distintos códigos. El método de factor de ráfaga simplifica la estimación de las respuestas debidas a las fuerzas estáticas, fluctuantes, y de auto-excitación aeroelástica, que se emplean para diseño y la revisión del estado último de falla. Cabe mencionar, que el problema de inestabilidad por aleteo generado por las fuerzas de auto-excitación aeroelásica puede limitarse revisando la velocidad de aleteo crítica del viento.

La normatividad actual de diseño de puentes en México (SCT, 2001) incluye un capítulo para el diseño ante acciones del viento sobre estas estructuras donde se presentan mapas de contorno de velocidades de viento, que sirven para evaluar la presión de viento para diseño y que se emplea junto con un factor de carga de 1.3 (β_VE × γ = 1.3); este factor, pudo haberse obtenido con alguna relación proporcional al factor de carga de 1.4 recomendado en las normas AASHTO (Rascón, 1999; AASHTO, 1994), sin embargo no existe un reporte detallado de la calibración de este factor para las condiciones mexicanas.

En este artículo se presenta una reseña de un trabajo previo (García-Soto et al., 2011), donde se proponen disposiciones de diseño, y se efectúo un trabajo de calibración, para diseñar puentes en México para un nivel de confiabilidad preestablecido. El objetivo principal de este estudio es emplear la propuesta de diseño desarrollada anteriormente y realizar un ejemplo de aplicación para un puente determinado, comparando la propuesta de diseño, con la normatividad de SCT (2001), así como con el reglamento estadounidense (AASHTO, 2007) y el canadiense (CAN/CSA-S6-06, 2006).

2.- DISPOCISIONES DE DISEÑO Y FACTORES DE CARGA PROPUESTOS

2.1 Resumen de la propuesta

En esta sección se presentan disposiciones de diseño que se proponen para el diseño de puentes por carga de viento para México, junto con factores de carga y resistencia que se orientan a la búsqueda de diseños con un nivel de confiabilidad preestablecido que sea uniforme para una amplia gama de casos de diseño.

La justificación racional del factor de carga de viento en la normatividad actual para el diseño de puentes en México no está esclarecida, y se carece de una calibración con base en la confiabilidad estructural que le de sustento. Tampoco se recomienda algún criterio limitante para la inestabilidad por aleteo. Los resultados de una calibración con base en la confiabilidad estructural en un estudio previo, se usaron para sugerir factores de carga de viento y factores de diseño para inestabilidad por aleteo. Se proporcionaron ecuaciones para calcular los factores de carga como funciones del coeficiente de variación de la velocidad del viento y de niveles de confiabilidad preestablecidos, ya que el uso del coeficiente de variación en tales ecuaciones, conllevaría a la consecución de diseños más consistentes desde la perspectiva de la confiabilidad estructural; además, las sencillas ecuaciones que se plantean para calcular los requeridos factores de carga de viento, podrían facilitar la labor de los desarrolladores de reglamentos de diseño (García-Soto, 2010; García-Soto et al.,2011).

2.2 Respuesta de los puentes ante las cargas de viento

Las excitaciones por unidad de longitud de la superestructura de un puente se pueden agrupar en la fuerza de arrastre D(t), fuerza de levantamiento L(t) y momento debido a cabeceo M(t), y pueden expresarse como (Simiu y Scanlan 1996),

\( D(t) = D_s + D_b(t) + D_{ae}(t) \) (1)

\( L(t) = L_s + L_b(t) + L_{ae}(t) \) (2)

\( M(t) = M_s + M_b(t) + M_{ae}(t) \) (3)

Donde los subíndices s, b, y ae representan la fuerza estática promediada en el tiempo, la fuerza de golpeteo (conocida en inglés como buffeting), y fuerzas aeroelásticas de auto-excitación, respectivamente. Una representación esquemática de estas fuerzas sobre en tramo de superestructura se muestran en la Figura 1. Las fuerzas aeroelásticas de auto-excitación pueden provocar inelastabiliad por aleteo (flutter-instability) si la velocidad del viento es mayor que la velocidad crítica del viento para aleteo, u_cr (Scanlan and Jones 1990). El caso muy conocido de la falla del puente Tacoma Narrows se asocia a este tipo de inestabilidad (Billah y Scalan, 1991).

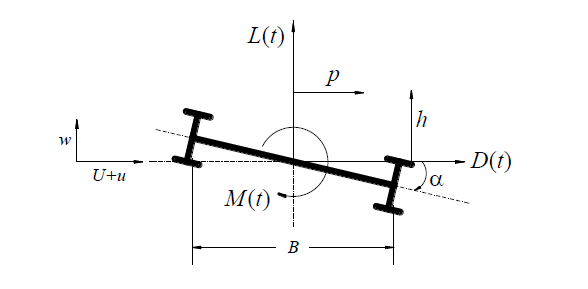
Fig. 1 Representación esquemática de las acciones del viento sobre un tramo de superestructura

La estimación de la respuesta debida a viento para velocidades por debajo de u_cr, se simplifica considerablemente si se emplea el concepto de factor de ráfaga y la teoría cuasiestática desarrollada por Daventport (1962). En tal método, las respuestas cuasiestáticas debidas al viento son iguales a las respuestas inducidas por la velocidad media del viento multiplicadas por un factor de ráfaga. También se ha desarrollado una derivación simplificada de la teoría del factor de ráfaga para evaluar la respuesta de puentes (Davenport 1981; Davenport and King 1982), en la que un puente se representa como una viga simplemente apoyada, y para la que el factor de ráfaga bajo el efecto de excitaciones en la dirección del viento, estaría dado por

\( g_T = 1 + (I_y \pi \bar{\sigma}_p) g_p \) (4)

donde I_u denota la intensidad de turbulencia de la fluctuación longitudinal,g_p es el factor pico, y la desviación estándar normalizada ˜σ_p se obtiene como

\( \bar{\sigma}_p = \bar{\sigma}_0(b, c', f_1) \) (5)

donde

\( \bar{\sigma}_0(b, c', f_1) = \sqrt{ \frac{1}{\pi^2/4 + L/\lambda} + \frac{1}{\pi^2/4 + c'f_1} \frac{\pi}{4(\xi + \xi_a)} bf_1^{-2/3} } \) (6)

y ξ es el porcentaje de amortiguamiento crítico (para el primer modo de vibración). En el desarrollo de la Ec. (6), se introduce una escala de turbulencia asociada al claro del puente, λ, igual a 60 m ; se incorpora el amortiguamiento aerodinámico ξ_a; f₁ = zω₁ /(2πU) ; ω₁ es la frecuencia del primer modo de vibración (de flexión horizontal); U es la velocidad del viento media horaria; c'=C_uL/z C_u es el coeficiente de decaimiento exponencial para la coherencia en función del claro de las fluctuaciones en la dirección del viento; L(m) es la longitud del claro del puente; z (m) es la elevación de la superestructura; y el valor del parámetro b es igual a 0.045 si se considera es espectro de Daventport.

A lo largo del estudio se consideró que la velocidad media del viento representaba la velocidad media horaria del viento, no obstante, al presentar las expresiones de diseño, también se dieron las equivalentes a un promedio de 3 s en la velocidad del viento, para hacerlas consistentes con la velocidad empleada en la normatividad mexicana. Un estudio paramétrico que empleó el uso de elementos finitos (Hu, 2009), mostró que la Ec. (6) se puede mejorar reemplazándola con esta otra ecuación

\( \bar{\sigma}_0(b, c', f_1) = \sqrt{ \frac{1}{\pi^2/4 + 0.025c'} + \frac{1}{\pi^2/4 + c'f_1} \frac{\pi}{4(\xi + \xi_a)} bf_1^{-2/3} } \) (7)

donde b = 0.049 si se usa el espectro de Kaimal (Kaimal et al., 1972) en lugar de el de Daventport. Un resumen de las ecuaciones y una de las gráficas proporcionadas por Hu (2009) que se pueden usar para evaluar las respuestas horizontales, verticales, y torsionales en la dirección paralela al viento y perpendicular al viento, se muestran en la Tabla 1, y la Figura 2.

Tabla 1 Ecuaciones para estimar las desviación estándar de la respuestas ante viento (de Hu, 2009)..

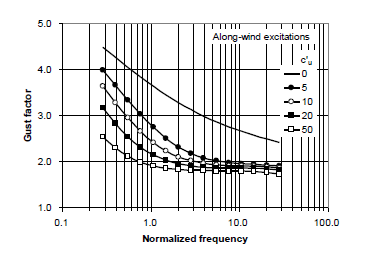
Fig. 2 Gráfica del factor de ráfaga (para ξ = 0.5% y ξ_a = 0) (reproducido de Hu, 2009).

El factor pico g_p que proporciona Hu (2009) (para c' mayor que cero) se puede aproximar con,

\( g_p = 4.0 + 0.16 \ln(f_1) \) (8)

Nótese que aunque las expresiones proporcionadas por Hu (2009) (ver también Hu et al.,2011) sirven para calcular tanto la respuesta horizontal, como la vertical y la torsional de la estructura, en ese trabajo se concluye que la desviación estándar normalizada, el factor pico, y el facto de ráfaga siguen las mismas tendencias, y de hecho, las Ecs. (4), (7), y (8) pueden utilizarse independientemente de la repuesta que se trate. Incluso el factor de ráfaga podría considerarse el mismo para las tres respuestas (horizontal, vertical, y torsional).

De hecho, el código canadiense (CAN/CSA S6-06, 2006) emplea el mismo factor de ráfaga para la consideración de cargas horizontales y verticales conjuntamente, e incluso la de momento torsionante, si se considera que en dos de los cuatro escenarios de cargas por viento planteadas en el reglamento canadiense, la carga vertical se aplica como una línea excéntrica respecto al eje longitudinal de la superestructura (ver sección 3.3 de este artículo). Esto implicaría dos posibilidades de implementación de metodología de diseño.

Una de las posibilidades sería la establecida en las normas CAN/CSA S6-06, donde básicamente se utiliza el factor de ráfaga para calcular la carga de viento horizontal, y ese mismo factor de ráfaga se emplea para calcular la carga de viento vertical aplicada excéntricamente o no (i.e., el momento torsionante, de alguna manera tiene implícito también el mismo factor de ráfaga).

La otra posibilidad sería la de obtener tres factores de ráfaga para calcular las correspondientes cargas horizontal, vertical, y momento torsionante, y aplicar estas tres cargas a la superestructura, considerando que tanto la carga vertical como el momento torsionante pueden actuar en un sentido o en otro (alternativamente se podrían usar el mismo factor de ráfaga en este caso, si las diferencias al calcularlo para los tres tipos de respuesta no son significativas). Antes de finalizar este apartado, mencionaremos algunos aspectos más.

Nótese que la respuesta pico es una variable con incertidumbre y se puede modelar como una variable tipo Gumbel (Davenport 1962). Dado que los resultados de análisis probabilísticos (Hong et al. 2001) mostraron que esta incertidumbre afecta la confiabilidad estructural solo marginalmente, tal incertidumbre no fue tomada en cuenta. La Respuesta pico media evaluada empleando el factor de ráfaga se utiliza para definir la carga de viento en el CAN/CSA S6-06 (2006), donde la carga de viento horizontal W se especifica en el siguiente formato,

\( W = C C_c C_h C_g U^2 \) (9)

donde C denota el coeficiente de análisis, C_e, C_h y C_g denotan los coeficientes de exposición, de arrastre horizontal, y de ráfaga, en el cual C_g corresponde al coeficiente gT mencionado anteriormente. Nótese que la carga de viento vertical sigue un formato análogo, excepto que el coeficiente de arrastre horizontal, es substituido por un coeficiente de arrastre vertical C_v (ver sección 3.3 de este estudio).

Adviértase que el coeficiente de análisis C, incluye tanto la densidad del aire, como el área de exposición. Una descripción mas explicita para calcular las fuerzas de viento para diseño, se desarrolla en la sección 3.3 de este artículo; esta descripción también puede ser útil si se desea calcular las fuerzas de viento para la propuesta reseñada para el caso de puentes en México (ver también la Figura 8). Adviértase también que el formato adoptado en la propuesta de diseño (García-Soto, 2010) podría diferir del que interesase a los desarrolladores de reglamentos en México, en cuyo caso se podrían realizar los ajustes pertinentes para hacerlo consistente con algún otro formato que se desee.

Finalmente, cabe mencionar que el estudio de Ge y Tanaka (2000) se puede encontrar una comparación de la exactitud de las ecuaciones para evaluar la velocidad crítica de inestabilidad por aleteo, ucr, la cual se puede también determinar con pruebas experimentales en túneles de viento de capa límite. Para evaluar ucr numéricamente, un puente se puede modelar mediante elementos finitos, y las fuerzas aeroelásticas de autoexcitación que actúan sobre el puente se pueden expresar en términos de matrices de rigidez y amortiguamiento aeroelásticas. Además, ucr se puede también identificar mediante un análisis de eigenvalores (e.g. Hua et al., 2007).

2.3 Modelos probabilísticos y consideraciones de diseño

En códigos con el formato de estados límite se considera la incertidumbre en los elementos mecánicos debidos a carga muerta y carga de viento, así como en la resistencia de los materiales, mediante el empleo de factores de carga y resistencia calibrados para estados limite determinados y niveles de confiabilidad predeterminados. Aunque en la normatividad mexicana (SCT, 2001) se indican especificaciones para carga de viento, no está disponible una documentación detallada que la justifique racionalmente. Por lo tanto algunas de las disposiciones de diseño proporcionadas en el CAN/CSA S6-06 (2006) se adoptaron para el análisis probabilístico y la calibración de factores de carga. Se consideraron modelos de resistencia apropiados para la práctica mexicana y las condiciones climatológicas de viento en México.

Si se considera que en el formato de diseño de estados limite, el diseño por carga de viento mas carga muerta (o carga muerta sola si ésta rige el diseño) satisface el requerimiento mínimo de resistencia, se puede plantear

\( R_D = \max(\alpha_D D_n, \alpha_D D_n + \alpha_W W_n) \) (10)

donde R_D es la resistencia de diseño factorizada, α_D0 es el factor de carga muerta cuando la carga muerta actúa sola, α_D es el factor de carga muerta y α_W es el factor de carga de viento, D_n es la carga muerta nominal, y W_n es la carga de viento nominal. La función de estado límite de falla, g₁, se puede escribir como,

\( g_1 = R - (D + W) \) (11)

donde R denota la resistencia, D denota el elemento mecánico debido a carga muerta, W representa el elemento mecánico debido a carga de viento, y g₁ <0 implica falla. Para estimar la probabilidad de que g₁ <0, los modelos probabilísticos para definir R, D y W se deben asignar y justificar. Para esa asignación y justificación de modelos, el lector es referido a un trabajo previo (García-Soto, 2010); en este estudio solo se presenta la Tabla 2 que resume los modelos adoptados. No obstante, si se señala muy brevemente la parte que concierne a la caracterización de la incertidumbre en las velocidades de viento que corresponden al entorno mexicano.

Tabla 2. Modelos probabilísticos empleados para la calibración

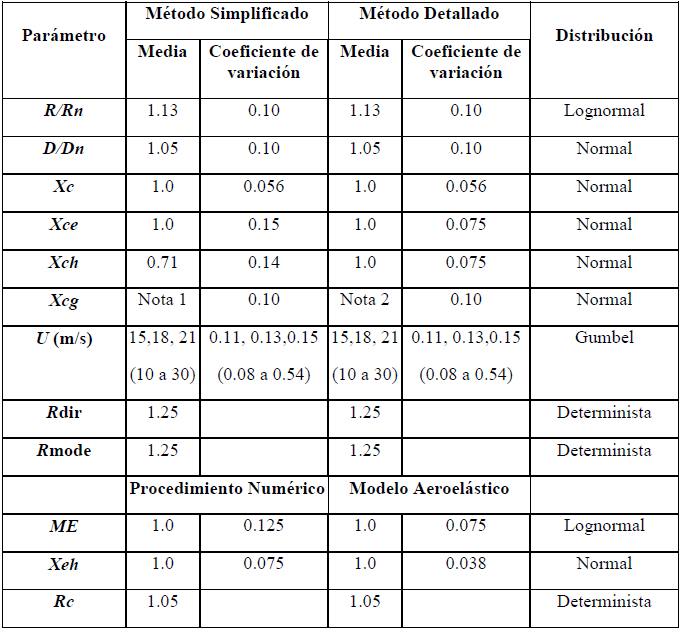
Nota 1: Para el método simplificado, la media de X_cg, m_xcg, está dada por el cociente de g_T evaluado en la velocidad del viento muestreada y a la altura de la superestructura para el valor de reglamento igual a 2.
Nota 2: Para el método detallado m_xcg, está dada por el cociente g_T evaluado en la velocidad del viento muestreada y a la altura de la superestructura entre el evaluado en la velocidad de viento de diseño a la altura de la superestructura.

El manual de diseño de obras civiles en una edición anterior (MOC, 1993) proporciona mapas de contorno de velocidades de viento para México. Cuando la propuesta de diseño se realizó, los mapas estaban siendo actualizados (López-López et al., 2008) y se basaron en una velocidad promedio en el tiempo de 3 s. No se tienen disponibles los datos estadísticos usados para desarrollar los mapas de contorno, pero con base en la información para la velocidad media del viento para periodos de retorno de 10, 50, y 200 anos en alrededor de 130 sitios, recomendada en la nueva versión del manual (MOC, 2008), y asumiendo que la velocidad máxima anula del viento está caracterizada por una distribución tipo Gumbel, se obtuvieron los mapas de contorno para los valores asociados a un periodo de retorno de 50 años para la velocidad máxima anual media del viento (promediada en el tiempo para 3 s). Este mapa se muestra en la Figura 3, junto con los mapas de los correspondientes valores medios, m_v, y coeficientes de variación, v_v.

Nótese que la velocidad del viento promediada en el tiempo para 3 s es igual a la velocidad media horaria del viento multiplicada por 1.52 (Durst, 1960), y que la velocidad máxima anual media del viento asociada a un periodo de retorno de T años, u_T, en términos de m_v y v_v está dada por

\( u_T = m_y \left( 1 - \frac{\sqrt{6 v_r}}{\pi} \left( 0.577 + \ln \left( -\ln \left( 1 - \frac{1}{T} \right) \right) \right) \right) \) (12)

Los modelos probabilísticos asignados a las variables con incertidumbre se adoptaron para el análisis de confiabilidad y para la calibración de factores de carga para niveles de confiabilidad preestablecidos.

Considerando que la carga de viento nominal se basa en la Ec. (9) y tomando como velocidad nominal del viento la correspondiente a la velocidad media para un periodo de retorno de 50 años, y que la resistencia R_D es igual a φR_N, donde R_N es la resistencia nominal y φ es el factor de resistencia, la función de estado límite (Ec. (11)) se puede reexpresar como,

\( g_1 = \frac{1}{\phi R_m} \frac{R}{\max(\alpha_{D0}, \alpha_D + \alpha_W \gamma)} \left( \frac{D}{D_n} + \gamma \frac{X_c X_{ce} X_{ch} X_{cg}}{R_{dir} R_{mode}} \left( \frac{U}{u_{50}} \right)^2 \right) \) (13)

donde X_c, X_ce, X_ch y X_cg son los cocientes de C, C_e, C_h and C_g entre sus valores nominales correspondientes; γ es el cociente de la carga de viento nominal entre la carga muerta nominal; y U es la velocidad máxima anual del viento modelada como una distribución tipo Gumbel. R_dir=1.25 y R_mode=1.25 para el método simple y, R_dir=1.0 y R_mode=1.25 para el método detallado (Bartlett and King, 2002). Se usó φ igual a 0.9 (NTCS, 2004).,

Para evaluar P( g₁ ≤0 ) se utilizó una técnica de simulación (Hu, 2009); se consideró una vida útil de 75 años para evaluar g₁≤0 , es decir P₇₅(g₁ ≤0 ) y se calculó el índice de confiabilidad correspondiente al mismo periodo de servicio, esto es

\( \beta_{75} = \Phi^{-1} (1 - P_{75} (g_1 \leq 0)) \) (14)

donde Φ^-1() es la inversa de la función estándar de distribución normal.

a) Valores asociados a un periodo de retorno de 50 años (Km/hr)

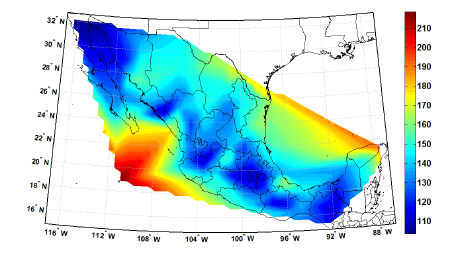
b) Velocidad máxima anual media del viento (Km/hr)

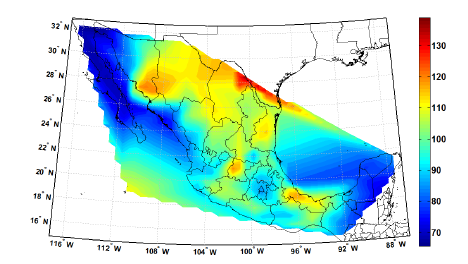
c) Coeficiente de variación de la velocidad máxima anual del viento

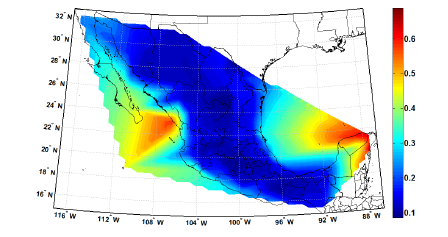
Figura 3. Mapas de contorno de peligro eólico en México (velocidad del viento para 3 s) con base en información del MOC (2008): a) valores para periodo de retorno de 50 años, b) Media, c)Coeficiente de variación.

Para el caso de inestabilidad por aleteo, se considero que el criterio limitante satisface

\( u_{\sigma} > \alpha_F R_c R_{we} u_{50} \) (15)

y que la función de estado limite , g2, se puede expresar como,

\( g_2 = M_E \frac{X_{we}}{\alpha_F} \left( \frac{U}{u_{50}} \right) \) (16)

donde α_F es el factor de diseño para estimar la inestabilidad por aleteo; el cociente de la velocidad media del viento para una promedio en el tiempo de 10 minutos o mayor, entre la velocidad media horaria del viento, R_c, se toma conservadoramente igual a 1.05; C_we es el factor de exposición para estimar la velocidad del viento a la altura de la superestructura; M_E denota un error de modelación global; X_we es el cociente de C_we respecto a su correspondiente valor nominal; y U es la velocidad máxima anual media horaria del viento.

Para una descripción más detallada, el lector interesado puede consultar a García-Soto (2010) o García-Soto et al. (2011).

2.4 Resultados de los análisis de confiabilidad

De manera muy sucinta se presentan a continuación los resultados de la calibración realizada. Aquí también, si el lector estuviera interesado en una descripción más detallada, podría consultarla en estudios anteriores (García-Soto, 2010; García-Soto et al., 2011).

Del análisis de confiabilidad y la calibración realizadas se proponen un método simplificado con un factor de carga de viento igual a 1.35, y un método detallado con un factor de seguridad, función del coeficiente de variación del viento y de un índice de confiabilidad seleccionado, como se indica en la siguiente ecuación

\( \alpha_W = 0.85 + (4.7 - 4.7 \times \beta_T + 1.6 \times \beta_T^2) v_r \) (17)

La figura 4 ilustra los niveles de confiabilidad obtenidos mediante el empleo de los factores de carga sugeridos.

Para el caso de inestabilidad por aleteo se propone un factor α_F definido en términos del coeficiente de variación y del índice de confiabilidad como

\( \alpha_F = 0.96 + 0.22 \times \beta_{T-75} - 1.51 \times v_r + 1.13 \times \beta_{T-75} v_r \) (18a)

para un método numérico, y si el método es experimental, con la siguiente ecuación

\( \alpha_F = 0.98 + 0.13 \times \beta_{T-75} - 1.36 \times v_r + 1.13 \times \beta_{T-75} v_r \) (18b)

Un ajuste de estas ecuaciones se puede apreciar en la Figura 5.

La tabla 3 muestra un resumen de la propuesta para diseño de puentes en México, que pueden compararse con lo estipulado en la normatividad actual para diseño de puentes en México (SCT, 2001) mostrada en la Tabla 4.

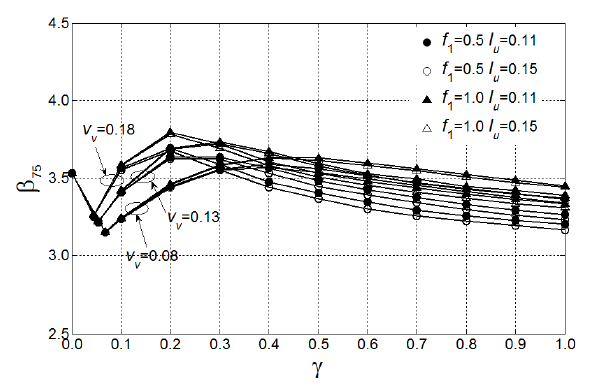
Figura 4. Índices de confiabilidad estimados

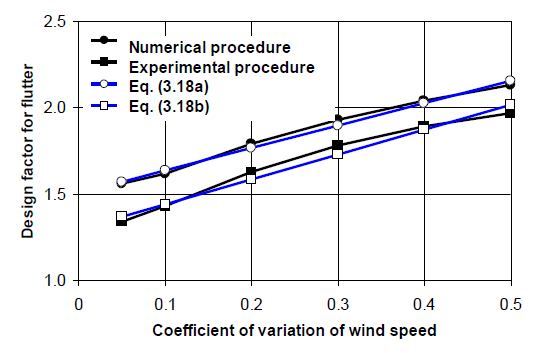
Figura 5. Factor de diseño para inestabilidad por aleteo para un índice de confiabilidad de 2.5 para un periodo de servicio de 75 años.

Tabla 3. Propuesta de diseño para puentes mexicanos

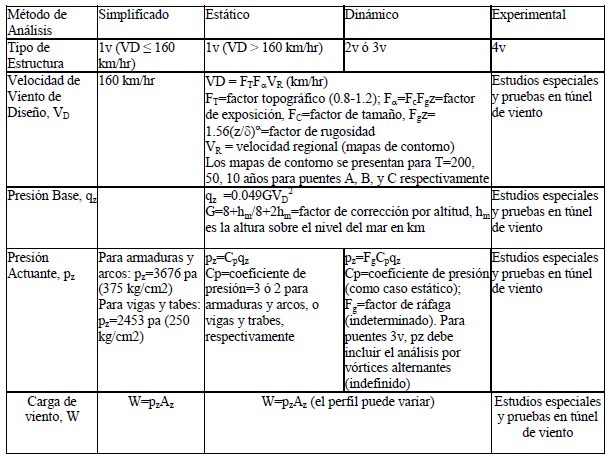
Tabla 4. Diseño por viento en la normatividad vigente (SCT, 2001)

3.-REGLAMENTOS CONSIDERADOS

Para este trabajo se consideraron los códigos mexicano (SCT, 2001), canadiense (CAN/CSA-S6-06, 2006) y estadounidense (AASHTO, 2007) de diseño de puentes. El código de la Comisión Federal de Electricidad (CFE) que es usado en México para el diseño de estructuras civiles, no ha sido incluido en este trabajo considerando que se tiene la normatividad de la Secretaría de Comunicaciones y Transportes para el diseño de puentes (SCT, 2001); no obstante, un estudio posterior podría incluir también la normatividad de la CFE. Este estudió se refiere primordialmente a los efectos del viento sobre la superestructura de puentes, aunque los temas abordados podrían incidir también en el diseño de otras partes de los puentes. La propuesta de diseño descrita en la sección 2 de este artículo (“Disposiciones de diseño y factores de carga propuestos”) se compara con las metodologías de diseño por viento de los reglamentos reseñados en las líneas subsecuentes.

3.1 Normatividad SCT (2001)

La normatividad mexicana para diseño de puentes (SCT, 2001) propone el diseño de estas estructuras dependiendo de su importancia (Tipos A, B, C), ya que la velocidad de regional para diferentes periodos de retorno (T_R) que se emplea para diseño, depende de esta clasificación (T_R = 200, 50, y 10 años, para estructuras Tipos A, B, y C, respectivamente). Además de la clasificación por importancia, se define otra clasificación relacionada con la respuesta de las estructuras ante la acción del viento (puentes 1v, 2v, 3v, ó 4v); está clasificación, junto con otras características, determina el tipo de método se puede emplear para diseño dentro de los contenidos en la propia normatividad: método simplificado, método estático, método dinámico, o métodos experimentales. Las velocidades regionales del viento que se requieren para determinar la velocidad de diseño, se presentan en mapas para diferentes periodos de retorno, y se menciona en la norma que corresponden a la velocidad que ocurre a una altura de 10 m sobre la superficie de un terreno de campo abierto en lomerío con algunas obstrucciones (SCT, 2001). Esta información parece tener sustento en los mapas de velocidades de viento de alguna versión anterior del Manual de Obras Civiles (MOC, 1993) de la CFE, mapas que fueron determinados para vientos de ráfaga para un promedio de 3s. La velocidad de diseño (V_D) se calcula en base a la citada velocidad regional (V_R), un factor de topografía (F_T), y un factor de exposición (F_α). El factor de exposición a su vez depende de un factor de tamaño (F_C), y de un factor de rugosidad (F_rz) que es función de la altura del centro de gravedad del área expuesta sobre el nivel del terreno o del agua (z), una altura en la que la rugosidad ya no influye en la velocidad del viento (δ), y un exponente que determina la variación de la velocidad del viento con la altura (α) (SCT, 2001). La velocidad de diseño se usa para calcular la presión actuante (p_z) que depende de un coeficiente de presión (C_p) (igual a 2 para trabes y vigas, y 3 para armaduras y arcos), y de la presión dinámica de base a la altura z (q_z). La presión dinámica de base se calcula mediante el producto de una constante, la velocidad de diseño al cuadrado, y un factor de corrección (G) que es función de la altura sobre el nivel del mar (h_m). Las ecuaciones para calcular la fuerza del viento pueden verse de manera resumida en la Tabla 4 en la sección anterior de este estudio, así como en la Tabla 5, donde además se presentan las ecuaciones para los otros reglamentos empleados en el presente trabajo.

Tabla 5. Ecuaciones para determinar las presiones y fuerzas de viento

Una vez calculada la presión actuante, la fuerza del viento sobre la superestructura se determina con p_z actuando normalmente al eje de la estructura en el sentido horizontal, conjuntamente con una carga vertical lineal (igual a 0.8 p_z por el ancho en planta) orientada hacia arriba y actuando a 1/4 de la planta de la superestructura a partir de barlovento; este escenario de carga es prácticamente el mismo que el empleado en el AASHTO (2007). Cabe mencionarse que p_z también puede descomponerse si existe un ángulo de esviajamiento del viento; esta consideración también se ecuentra en el regalmento AASHTO (2007), y en el caso del reglamento canadiense, este ángulo (ángulo de “ataque” del viento) sólo se utiliza para la subestructura, ya que se considera que el caso crítico para la fuerza de viento horizontal es cuando este actúa perpendicular al eje de la superestructura (Comentarios de la CAN/CSA-S6-06, 2006). El método dinámico contenido en la normatividad de la SCT (2001) es análogo al método estático, salvo por la inclusión de un factor de ráfaga que al multiplicar a p_z la amplifica convirtiéndola en una carga estática equivalente. Adviértase que este factor no está determinado en la normatividad de SCT y se requiere de estudios experimentales para definirlo, mientras que en la propuesta de diseño presentada en el apartado 2 de este estudio (ver también García-Soto et al., 2011) si se determina expresamente la manera de incluirlo en los cálculos, tanto en el procedimiento simplificado, como en el detallado. Un aspecto más que hay que mencionar, es que la normatividad de la SCT (2001) menciona la necesidad de incluir los efectos de vórtices alternantes, y/o realizar métodos experimentales para las estructuras que lo requieran, aunque no se describen métodos o lineamientos, como es el caso del fenómeno de inestabilidad aeroelástica para el que no se presenta ninguna disposición del tipo de la incluida en el apartado 2 de este estudio.

Finalmente, el caso de carga básico que se considera en este trabajo es el de carga muerta más carga de viento, que para el caso de la SCT corresponde al Grupo II para factores de carga y se muestra en la Tabla 6, junto con las demás combinaciones de carga empleadas en este artículo. Debe señalarse que otros efectos, además de la carga muerta y carga de viento, no fueron considerados en ninguna de las combinaciones de carga de la Tabla 3 (e.g., flujo plástico, acortamiento por deformación, frenaje, efectos secundarios por preesfuerzo, temperatura, etc.).

Tabla 6. Factores de carga y combinaciones de acerdo a los reglamentos considerados

Nota: (1) Estos factores de carga son empleados en el método simplificado. Para el método detallado, el factor de carga para carga muerta es 1.25 y para carga de viento es igual a 2.81. Este último se determinó considerando un coeficiente β_T = 3.5 y un coeficiente de variación v_v = 0.25.

3.2 Reglamento AASHTO (2007)

El reglamento AASHTO (2007) emplea una ecuación, que se fundamenta en la ley logarítmica, para describir la variación de la velocidad media del viento con la altura, para determinar la velocidad de viento de diseño (V_DZ) para puentes a una altura mayor a 10 m sobre el terreno o el nivel de agua. Esta velocidad está en función de la altura de la superestructura (Z), de la velocidad del viento a 10 m sobre el terreno o nivel de agua (V₁₀), una velocidad de viento base de 160 km/hr (V_B), así como una velocidad y longitud de fricción que incluyen consideraciones meteorológicas y ubicación de la estructura (V₀ y Z₀, respectivamente). Se señala que cuando el viento es la condición crítica de diseño, se deben investigar las variaciones en el viento debido a las condiciones locales, y también se recomiendan pruebas en túnel de viento para obtener estimaciones más precias cuando el viento rija el diseño (AASHTO, 2007). V₁₀ se puede determinar de muestreos locales del viento, de la información contenida en el ACSE 7-88, o ser considerada igual a 160 km/hr en ausencia de un mejor criterio. Parece ser que el tiempo promedio para determinar las velocidades en el ASCE 7-88, y la velocidad base V_B = 160 km/hr en el AASHTO (2007) se determinaron para un promedio de la velocidad del viento con base en la “milla más rápida”. Para calcular la presión del viento sobre las estructuras, se asume que la carga actúa horizontalmente y que la presión de viento de diseño (P_D) se puede determinar como el producto del cuadrado del cociente de la velocidades de diseño entre la velocidad base por una presión base de diseño (P_B) que cambia dependiendo del tipo de superestructura que se tenga y que puede actuar sólo en el barlovento, o bien tanto en el barlovento como en el sotavento; para el caso que se verá más adelante en este estudio, esta presión base es igual a 0.0024 Mpa actuando únicamente en el barlovento. Aunque en el AASHTO (2007) no se emplea expresamente un factor de ráfaga en la determinación de las fuerzas de viento, de la lectura de las normas se puede inferir que el factor de ráfaga está implícito en la presión base, ya que se indica que la presión de estancamiento asociada a una velocidad de 160 km/hr es igual a 1.23 × 10^-3 Mpa. Con base en la definición de presión dinámica (1/2ρV² = 1.21E-3 (MPa)), se podría inferir que un factor de ráfaga igual a 2 está implícito en P_B = 0.0024 Mpa. La misma conclusión se puede derivar para otras presiones base contenidas en el AASHTO (2007). El reglamento indica que la carga de viento calculada no debe ser menor que 4.4 N/mm sobre el claro de vigas o trabes; restricciones similares se indican para otras estructuras. Si el viento no actúa de manera normal a la estructura, se presentan presiones base en función del ángulo “de ataque”. Para la combinación de cargas básica considerada en este estudio, correspondiente a la combinación de estado límite de carga III de las AASHTO (2007), “Resistencia III”, se debe incluir además de la carga de viento horizontal (y sólo cuando está actúa ortogonalmente a la estructura), una carga lineal vertical actuando hacia arriba y localizada a 1/4 de la superestructura a partir del barlovento; esto es análogo al caso de la normatividad de la SCT (2001), como se indicó previamente. Se indica que los efectos de las fuerzas aeroelásticas deben considerarse para estructuras “sensibles al viento” (AASHTO, 2007), y se da la recomendación de considerar como estructuras sensibles a aquellas que presenten una relación de aspecto del claro entre el ancho o el peralte de la superestructura de más de 30. Está recomendación también aparece en la normatividad de la SCT (2001). A los desarrolladores de reglamentos de diseño, podría interesarles lo recomendado en los comentarios del reglamento canadiense (Comentarios de la CAN/CSA-S6-06, 2006), donde además de la recomendación en base a la relación de aspecto, se dan otros lineamientos para determinar si la estructura es “aeroelásticamente sencsible”, y que están en función de amortiguamiento aerodinámico, la respuesta dinámica ante turbulencia, o la relación de la frecuencia fundamental de vibración de torsión entre la vertical (donde un valor menor a 1.4 sería indicativo de una potencial inestabilidad por aleteo). El lector interesado es referido a las páginas 85 y 86 de la parte de cargas en los comentarios del reglamento canadiense de diseño de puentes (Comentarios de la CAN/CSA-S6-06, 2006). En lo que respecta a la inestabilidad por aleteo (conocida en inglés como flutter), el AASHTO (2007) menciona que los puentes deben diseñarse para no presentar divergencia e inestabilidad por aleteo (flutter) hasta 1.2 veces la velocidad de viento de diseño aplicable a la altura de la superestructura. En lo que concierne a la revisión de los estados límite de falla considerando factores de carga y resistencia, el AASHTO sigue el conocido formato (y que de hecho es el mismo formato, con algunas variantes, para todas las propuestas comparadas en el presente artículo) que se índica a continuación:

\( \sum \eta_i \gamma_i Q_i \leq \phi R_n \) (19)

donde η_i es un factor producto de otros factores que toman en cuenta la importancia, redundancia, y ductilidad de la estructura (en este estudio se considera igual a 1, correspondiendo a un índice de confiabilidad β = 3.5); γ_i es un factor de carga; Q_i es un elemento mecánico producido por las cargas especificadas en el reglamento; φ es un factor de resistencia; y R_n es la resistencia nominal para el elemento mecánico considerado en el diseño. En las tablas 5 y 6 se muestran de manera sucinta las ecuaciones y combinación de carga de las AASHTO empleadas en este trabajo.

3.3 Reglamento CAN/CSA-S6--06 (2006)

A diferencia de los códigos anteriores, el reglamento canadiense (CAN/CSA-S6-06, 2006) no proporciona velocidades, sino presiones de diseño. No obstante, la presión de diseño media horaria (q) en pascales, se puede relacionar con la velocidad de diseño mediante la siguiente ecuación (Comentarios de la CAN/CSA-S6-06, 2006)

\( q = 0.05 V^2 \) (20)

donde V es la velocidad del viento media horaria en km/hr. Esta expresión resulta útil si se quiere realizar un ejercicio de comparación como el del presente estudio, ya que la información proporcionada en otros reglamentos (e.g., SCT, 2001; AASHTO, 2007) está dada en términos de velocidades. Adviértase sin embargo, que si la velocidad del viento de otro reglamento (e.g., SCT, 2001) está dada con base a promedios de tiempo diferentes (e.g., 3 s), habría primero que hacer la conversión correspondiente (Durst, 1960), de tal manera que la información empleada sea consistente con el código considerado. De manera similar, habría que procurar que se utilice el periodo de retorno que el reglamento correspondiente considere asociado a la velocidad de viento nominal, para una determinada estructura. Más aun, si se quiere hacer una comparación entre reglamentos lo más consistente posible, también debe conocerse para que nivel de confiabilidad fueron propuestos los modelos nominales y los correspondientes factores de carga y resistencia para los estados limite de falla en estudio. Con todo esto, aun es necesario tener en cuenta que las características geográficas, de producción y fabricación de materiales, la mano de obra, etc., varían significativamente de un país a otro, y aun de una región a otra (i.e, los datos estadísticos y las distribuciones de probabilidad de las cargas y las resistencias variaran de un lugar a otro), por lo tanto una comparación racional entre distintos reglamentos, debería tener estos aspectos en consideración.

Regresando a la metodología del reglamento canadiense, la presión de diseño media horaria de referencia mencionada anteriormente (q), será la calculada para un periodo de retorno que depende de la longitud del claro del puente: 100 años para puentes con algún claro igual o mayor que 125 m, y 50 años para puentes con claros máximos no mayores de 125 m; otros periodos de retorno aplican para luminarias, barreras, otros accesorios, estructuras en etapas constructivas, etc. (CAN/CSA-S6-06, 2006). Se menciona en el reglamento que si el sitio donde está ubicada la estructura puede propiciar la ocurrencia de un efecto de “embudo”, la presión de referencia debe incrementarse en 20%.

Se recomienda en el reglamento canadiense un factor de ráfaga C_g = 2, para puentes que no son muy susceptibles a la acción del viento, que incluyen la mayoría de puentes con claros menores de 125 m, excepto los puentes con cables. Para estructuras que son sensibles a la acción del viento, no debería emplearse el método de factor de ráfaga, y las cargas de viento deberían determinarse con base en un análisis detallado de la acción dinámica del viento mediante algún método acreditado que incluya los efectos del viento fluctuante (conocido en inglés como buffeting) (CAN/CSA-S6-06, 2006). Nótese que un método como el referido en las líneas anteriores, podría corresponder –por ejemplo- a la propuesta presentada en el apartado 2 de este estudio, bajo la descripción de “Método detallado” (ver Tabla 3).

El facto de exposición (C_e) no debe ser menor que 1, y se puede tomar de una tabla en el reglamento, o calcular con una ecuacion que es función de la altura desde el terreno hasta la parte superior de la superestructura (H).

Con la información anterior, la superestructura se diseña para cargas de viento verticales y horizontales actuando simultáneamente. Se asume que la dirección del viento debe ser perpendicular al eje de una superestructura recta, o perpendicular a un eje seleccionado en un puente curvo, de tal manera que se maximicen los efectos inducidos por el viento. La fuerza horizontal por unidad de área (en elevación) que debe aplicarse a la superestructura se calcula como un producto de q, C_g, C_e, y un factor de arrastre horizontal C_h = 2; algunas consideraciones adicionales en el factor de arrastre son estipuladas para el caso de puentes con armaduras. Análogamente, la fuerza vertical por unidad de área (en planta) que debe aplicarse a la superestructura se calcula como un producto de q, C_g, C_e, y un factor de arrastre vertical C_v = 1; la fuerza vertical debe ser aplicada ya sea hacia arriba o hacia abajo. Además de aplicar la carga vertical como una carga uniformemente distribuida sobre toda la planta de la superestructura, se debe tomar en cuenta el efecto de una posible excentricidad en la aplicación de las cargas. Para considerar lo anterior, se debe aplicar la misma carga total pero aplicada como una carga vertical equivalente sobre una línea ubicada a 1/4 de la superestructura a partir de barlovento. Esta consideración para las cargas de viento horizontales y verticales actuando simultáneamente, marca una diferencia significativa respecto de lo estipulado en el reglamento AASHTO (2007) y la normatividad SCT (2001). Mientras que en los códigos canadiense y mexicano se tiene solo un escenario de carga para a acción simultánea del viento en el sentido horizontal y en el vertical (con la carga vertical actuando únicamente hacia arriba a lo largo de una línea excéntrica sobre la superestructura), en el reglamento canadiense se tienen 4 casos, o escenarios, de carga: 1) carga horizontal más carga vertical uniformemente repartida actuando hacia arriba; 2) carga horizontal más carga vertical uniformemente repartida actuando hacia abajo; 3) carga horizontal más carga vertical actuando únicamente hacia arriba a lo largo de una línea excéntrica sobre la superestructura; y 4) carga horizontal más carga vertical actuando únicamente hacia abajo a lo largo de una línea excéntrica sobre la superestructura. Cabe mencionar que la aplicación de cargas excéntricas toma en consideración la posibilidad de volteo (Comentarios del CAN/CSA-S6-06, 2006).

La diferencia en los casos de carga mencionados arriba para las cargas de viento actuando simultáneamente en el caso del código canadiense respecto a los otros códigos considerados, tiene implicaciones importantes, ya que los elementos mecánicos inducidos a la superestructura serán distintos. Particular atención debería ponerse al caso en que la carga de viento vertical actúa hacia abajo, ya que para el caso básico de combinación de carga considerado en este estudio, los elementos mecánicos producidos por la carga muerta, se verían incrementados con la acción del viento; esto tiene implicaciones no solo en el diseño, sino en la calibración de factores de carga y resistencia adecuados para un determinado estado limite y un nivel preestablecido de confiabilidad. En el presente estudio, para la propuesta de diseño planteada en la sección 2, se adoptará lo estipulado en el reglamento canadiense para efectos de la acción simultánea de cargas de viento horizontales y verticales actuando simultáneamente sobre la superestructura. Lo anterior se justifica debido a que se siguió lo planteado en el CAN/CSA S6-06 (2006) para sugerir la propuesta de diseño, en virtud de la disponibilidad de los datos estadísticos utilizados para la calibración de los factores de carga y resistencia; valdría la pena investigar, si en la práctica existen evidencias de que algunas fallas o comportamiento inadecuado de puentes, asociadas a la acción conjunta de la carga muerta y la carga de viento actuando en la misma dirección.

Otro aspecto que vale la pena mencionar, es que el reglamento canadiense estípula que las cargas de viento deben también considerarse con una distribución no uniforme, es decir, una fuerza de viento puede estar actuando en una porción de la superestructura, y otra fuerza de viento (una fracción de la primera igual a 0.75) debe actuar en el resto de la superestructura. Esta consideración que podría ser critica en algunos casos, como por ejemplo en algunas etapas constructivas (Comentarios del CAN/CSA S6-06, 2006), no se incluyó en este estudio.

En el reglamento CAN/CSA-S6-06 (2006), se propone un criterio para revisar la inestabilidad aeroelástica de los puentes. Se debe mostrar que el comportamiento de la estructura, sin la aplicación de factores de carga, es aceptable hasta una velocidad del viento mayor que la velocidad de referencia del viento, Vref, Salvo que estén disponibles métodos alternativos razonables, la velocidad de referencia debe tomarse como:

\( V_{ref} = 1.24 \sqrt{\alpha_w q C_e} \) (21)

donde α_w es el factor de carga por viento que se definirá a continuación. Nótese que la carga de viento de referencia debe tomarse a la altura del tablero de la superestructura.

Si las cargas de viento de la estructura en su conjunto se determinan mediante pruebas en túnel de viento, el factor de carga por viento, α_w, se debe calcular como:

\( \alpha_w = 0.86 \delta_w \exp(3.5 k V_w) \) (22)

donde

\( k = \sqrt{\frac{V_w^2}{0.15^2 + V_w^2}} \) (23)

el coeficiente de sesgo (relación del valor medio entre el valor nominal), δ_w, y el coeficiente de variación, V_w, del elemento mecánico debido al viento debe ser determinado por las personas responsables de las pruebas en túnel de viento. Adviértase que en la propuesta presentada en este trabajo, se propone también un factor de carga por viento que es función del coeficiente de variación, pero también del índice de confiabilidad (García-Soto et al., 2011); esto esta basado en el estudio desarrollado por Hu (2009), donde también se encontró que el factor de carga en la Ec. (22), podría no conllevar al diseño de estructuras con un nivel de confiabilidad uniforme.

Antes de finalizar con este apartado, vale la pena mencionar alguno aspectos contenidos en los comentarios al reglamento canadiense de diseño de puentes (Comentarios del CAN/CSA S6-06, 2006). Entre la información importante se menciona que de acuerdo a pruebas no publicadas del túnel de viento de capa límite de la Universidad del Oeste de Ontario, indican que C_h=2 con base en el área completa frontal expuesta, es un valor conservador para superestructuras comunes con losa, trabes hechas de placas de acero, y secciones cajón. También se comenta que para la mayoría de tipos de superestructura, el valor prescrito de C_v=1 conlleva a valores conservadores tanto de las cargas verticales como de los momentos torsionantes alrededor del eje longitudinal. Un valor más grande de C_v podría ser apropiado si el ángulo de ataque cambia significativamente debido a la topografía local, por ejemplo en el caso de puentes cuyos claros libran una cañada profunda. Se menciona también, que está previsto que el elemento mecánico factorizado debido al viento obtenido mediante pruebas de túnel de viento, será aproximadamente del orden del 70% del obtenido usando métodos simplificados.

Las ecuaciones para calcular las cargas de viento, así como la combinación de carga con sus respectivos factores de carga y resistencia para el caso del código canadiense, también están resumidos en las Tablas 5 y 6.

Un último aspecto antes de terminar con la sección 3 de este articulo, es la consideración de vórtices alternantes, que si bien es mencionada por todos los reglamentos, en el sentido de que deben ser evaluadas las estructuras que se presuma sean sensibles a este efecto, no se presentan métodos descritos detalladamente para evaluar este fenómeno y su efecto en las estructuras de puentes, pero se le liga con problemas de fatiga que deberían ser evaluados.

4.- CASO DE APLICACIÓN

4.1 Antecedentes del puente y consideraciones de análisis

El puente Carrizo se ubica en la sierra madre occidental, cerca de la frontera de los estados de Sinaloa y Durango, en el kilómetro 162 + 720 de la nueva autopista Durango-Mazatlán. El puente se compone de dos cuerpos, uno atirantado y uno en doble voladizo, como se muestra en la figura 6.

El puente se modeló en el programa SAP200. Para la modelación del puente, se emplearon elementos barra, elementos shell y cables. Todos los elementos fueron caracterizados con las dimensiones de los elementos y materiales del proyecto ejecutivo. Para los análisis sólo se consideró el cuerpo en voladizo del puente, el cual tiene una longitud total de 75 m. La conexión del puente en voladizo y el puente atirantado se modeló como simplemente apoyada. Aunque lo anterior no es del todo correcto, es suficiente para los fines ilustrativos del presente estudio. La figura 7 muestra una imagen del modelo matemático del puente en voladizo.

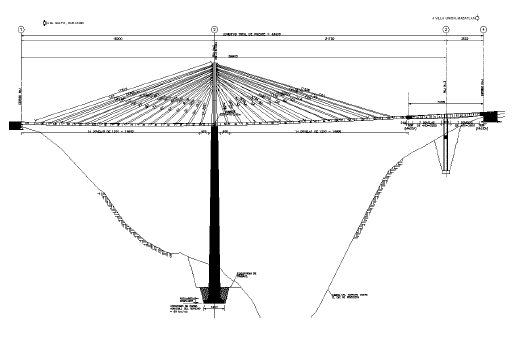
Figura 6. Puente Carrizo

Figura 7. Cuerpo en voladizo del puente Carrizo

Las cargas consideras en el modelo matemático fueron las de peso propio, carga de asfalto y la carga de viento en sus diferentes configuraciones. Los factores de carga y combinaciones empleados en los análisis son los mostrados en la Tabla 6.

Las configuraciones para la aplicación de las cargas de viento por cada reglamento y las propuestas en este estudio se presentan en la Figura 8.

Para la evaluación de las fuerzas del viento, se emplearon velocidades promedio del viento de acuerdo al tiempo de promediación sugerido por cada reglamento.

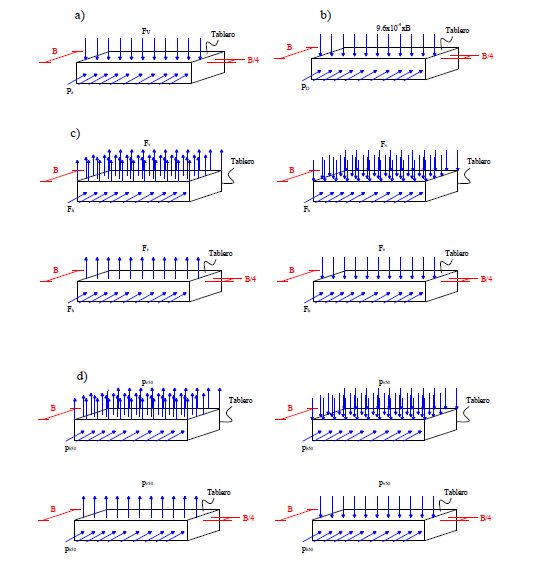
Figura 8. Configuraciones de la aplicación de las cargas de viento sugeridas por diferentes reglamentos y en este estudio: (a) SCT (2001); (b) AASHTO (2007); (c) CHBDC (2006); (d) Propuestas en este estudio.

4.2 Resultados de los análisis y comparación

La siguiente tabla presenta una comparación de los parámetros estimados para el cálculo de las fuerzas o presiones de viento sugeridas por cada reglamento.

Tabla 7. Comparación de parámetros para el cálculo de las fuerzas o presiones de viento sugeridas por cada reglamento

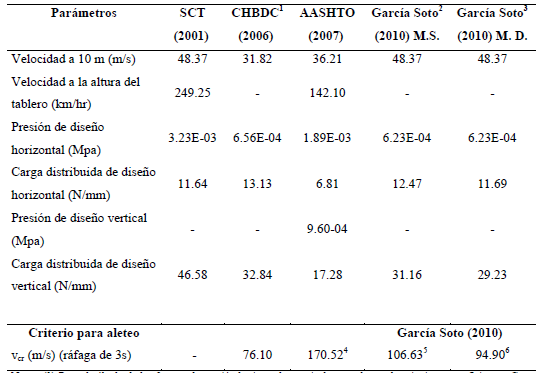
Notas: (1) Para el cálculo de las fuerzas de presión horizontal y vertical se emplearon los siguientes coeficientes: Ce = 1.42; Cg = 2; Ch = 2 y Cv = 1. Para el cálculo de la velocidad referencia del viento para el criterio de aleteo, se empleó un coeficiente de sesgo w = 1 y un coeficiente de variación Vw = 0.25.; (2) Para el método simplificado (M.S.), se emplearon los siguientes factores para determinar las fuerzas de diseño: Ce = 1.42; Cg = 2; Ch = 2 y Cv = 1. (3) Para el método detallado (M.D.), se asumieron los siguientes valores para el cálculo de las fuerzas del viento, a falta de resultados de túnel de viento: Ce = 1.42; Ch = 2 y Cv = 1. El valor del factor de ráfaga para el método detallado, considerando la frecuencia horizontal de vibrar es de Cg = 1.88. (4) Se determinó al multiplicar 1.2 por la carga de diseño a la altura del tablero. (5) y (6) Se consideró un valor de T75 = 3.5 y un coeficiente de variación vv = 0.25 para determinar el factor F, empleado para el cálculo de la velocidad crítica o de referencia.

Se observa de la tabla anterior que, en general, los valores de las presiones y cargas son similares, excepto por el caso del reglamento AASHTO (2007), en el que las presiones y fuerzas son relativamente menores. También se observa en la tabla que las velocidades críticas o de referencia para el criterio de aleteo de acuerdo al reglamento Canadiense y los métodos simplificado y detallado difieren un poco. Lo anterior se debe principalmente al factor de carga empleado en cada uno de los métodos para la estimación de la velocidad de aleteo. También se observa de la tabla que la velocidad de referencia sugerida por AASHTO (2007) resulta superior a las anteriores.

Para la comparación de resultados, empleando las fuerzas de viento y las combinaciones de carga resumidas en la Tabla 6, la siguiente figura identifica los puntos del puente estudiados. Para el punto 1 se estudió el desplazamiento horizontal (en dirección x), mientras que para el punto 2 se estudiaron los momentos flexionantes inducido por el viento (My y Mz).

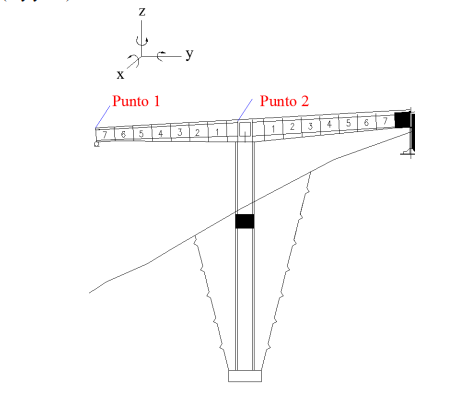
Figura 9. Identificación de puntos para el estudio de la respuesta.

La siguiente tabla presenta una comparación de las respuestas obtenidas en los puntos identificados en la figura anterior.

Tabla 8. Comparación de respuesta ante combinaciones de carga en la tabla 6.

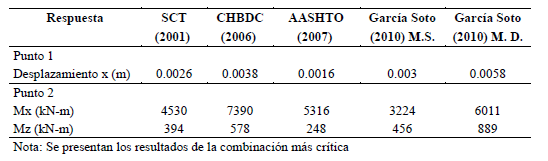
Se observa de la Tabla 8 que los desplazamientos inducidos por el viento ante las combinaciones estudiadas son consistentes. El valor del desplazamiento más bajo se obtuvo con la combinación sugerida por AASHTO (2007) y el más alto fue obtenido con el método detallado sugerido por García Soto (2010). También se observa en la tabla que los momentos flexionantes obtenidos son consistentes. El momento flexionante más grande alrededor del eje x se presentó para la combinación sugerida por el reglamento CHBDC (2006) y el más bajo cuando se emplea el método simplificado sugerido por García Soto (2010). Para el momento alrededor del eje y, el método detallado de García Soto (2010) proporciona el momento flexionante más grande, mientras que el AASHTO (2007) proporciona el más bajo. De la comparación de los resultados anteriores, se observa que la metodología detallada sugerida por García Soto (2010) ofrece una buena alternativa para su uso en el diseño de puentes convencionales. Además de la observación anterior, el método detallado también sugiere el valor de la velocidad de referencia para el criterio de aleteo. Lo anterior es importante, ya que la normativa mexicana actual no contempla la estimación de esta velocidad.

5.- CONCLUSIONES

Se llevo a cabo una descripción de un método propuesto para el diseño de puentes en México y la calibración de factores de carga conducentes a diseños para un nivel de confiabilidad preestablecido, con el que se alcanzará un nivel de confiabilidad uniforme para una amplia gama de casos de diseño de puentes. También se realizó una descripción y comparación de los reglamentos de diseño de puentes empleados en México, Estados Unidos, y Canadá, señalando algunos de los aspectos más relevantes de estos códigos en lo que respecta al diseño eólico de puentes. Las disposiciones de diseño propuestas, junto con lo estipulado en las otras normatividades citadas, se revisaron mediante un ejercicio de aplicación a una estructura de un proyecto real de un puente para la República Mexicana.

El método propuesto adoptó el formato del reglamento canadiense para llevar a cabo la calibración de factores de carga, ya que mucha de la información estadística sobre las variables con incertidumbre necesaria para realizar la calibración, estaba disponible para esa normatividad; no obstante, las características probabilísticas de las velocidades de viento y de las resistencias de materiales para México fueron incorporadas. Si fuera necesario, el formato podría ajustarse al que se emplea en algún(os) código(s) mexicano(s).

El reglamento de la SCT tiene similitudes con el reglamento estadounidense, sin embargo, no existe un reporte detallado de la calibración del factor de carga de viento para las condiciones mexicanas; tampoco presenta un criterio limitante para la inestabilidad aeroelástica. Las diferencias y similitudes entre los códigos usados están contenidas, y enfatizadas en el cuerpo de este trabajo, en el que también se mencionan algunos aspectos que no están dilucidados expresamente. Esta descripción podría ser útil tanto para diseñadores, como para desarrolladores de reglamentos de diseño.

Para el ejemplo de aplicación se trató de ser lo más consistente posible, por ejemplo, empleando la velocidad promediada en el tiempo en la que se basa cada reglamento; está velocidad está asociada a los periodos de retorno que se emplearon para definirla como velocidad nominal, ligada al nivel de confiabilidad preestablecido para cada código, con sus correspondientes factores y combinaciones de carga. Como era de esperarse, se presentaron diferencias en los valores de carga de cada reglamento, y en las solicitaciones impuestas a la estructura que se utilizó para el ejemplo de aplicación; sin embargo, se considera que la propuesta presentada para el diseño de puentes en México (García Soto, 2010), es la que conlleva a niveles de confiabilidad más uniformes, para las condiciones mexicanas, y para una amplia gama de casos de diseño. La comparación de resultados sugiere que el método detallado (García Soto, 2010) ofrece una buena alternativa para su empleo en el diseño por viento de puentes convencionales. Cabe mencionarse que lo estipulado en los diferentes reglamentos, muchas veces se estudia y calibra bajo consideraciones que no siempre son exhaustivas. Por ejemplo, muchos estudios se basan en la consideración de puentes simplemente apoyados de distintas longitudes; sin embargo, este no siempre es el caso de estructuras reales que pueden tener otras condiciones de apoyo (como el puente considerado en este trabajo); por lo tanto, siempre existe la posibilidad de extender los estudios de calibración a casos no cubiertos, para estimar el impacto de su inclusión/exclusión en los ejercicios de calibración.

El desarrollo en curso del proyecto de un túnel de viento de capa límite para México, sugiere que en el futuro se podría generar información estadística más cercana a las condiciones mexicanas de diseño, información que sería esencial para la calibración de futuros reglamentos mexicanos de diseño de puentes.

6.- AGRADECIMIENTOS

Se agradece al comité organizador del 1er Simposio Nacional de Ingeniería Eólica, a la Universidad de Guanajuato, y al Instituto de Ingeniería de la UNAM, por el apoyo económico y las atenciones brindadas. Agradecemos también a José Alberto Escobar por sus atinadas críticas, comentarios, y sugerencias.

7.- REFERENCIAS

AASHTO (1994). LRFD bridge design specifications. 1st edition, American Association of State Transportation Officials, Washington, DC.

AASHTO (2007). LRFD bridge design specifications. 4th edition, American Association of State Transportation Officials Washington D.C.

Bartlett, F. M., and King, J. P. C. (2002). Wind load factors for the Canadian Highway bridges design code. Developments in Short and Medium Span Bridge Engineering – 2002, I, 683-690

Billah, K., Scanlan, R. (1991). Resonance, Tacoma Narrows bridge failure, and undergraduate physics textbooks. American Journal of Physics 59 (2), 118–124.

CAN/CSA-S6-06 (2006). Canadian highway bridge design code, Canadian Standards Association, Toronto.

Commentarios del CAN/CSA-S6-06 (2006). Canadian highway bridge design code, Canadian Standards Association, Toronto.

Davenport, A. G. (1962). Buffeting of a suspension bridge by storm winds. Journal of Structural Engineering, ASCE 1962, 88(ST3), 233-68..

Davenport, A. G. (1981). Reliability of long span bridges under wind loading. ICOSSAR 81, Trondheim, Norway, June.

Davenport, A. G., and King, J. P. C. (1982). The incorporation of dynamic wind loads into the design specification for long span bridges. ACE Fall Convention and Structures Congress, New Orleans, Louisiana.

Durst, C. S. (1960). Wind speeds over short periods of time. Meteorological Magazine, 89, 181-

García-Soto, A. D. (2010). Probabilistic basis for recommending some Mexican bridge design load requirements. Ph.D. Thesis, Chapter 3. The University of Western Ontario, London, Ontario, Canada.

García-Soto, A. D., Hong, H. P., y Gómez, R. (2011). Reliability analysis of bridges under wind loads and their implication for Mexican highway bridge design. Proceedings of the 13th International Conference on Wind Engineering, ICWE13. Amsterdam, The Netherlands.

Ge, Y. J., and Tanaka, H. (2000). Aerodynamic flutter analysis of cable-supported bridges by multi-mode and full-mode approaches. Journal of Wind Engineering and Industrial Aerodynamics, Vol. 86, 123-153.

Hong, H. P., Beadle, S., and Escobar, J. A. (2001). Probabilistic assessment of wind-sensitive structures with uncertain parameters. Journal of Wind Engineering and Industrial Aerodynamics, 89(10), 893-910.

Hu, Z. (2009). Gust responses of bridges to spatially varying wind excitations and calibration of wind load factors. M.E.Sc. Thesis, University of Western Ontatio.

Hu, Z., Hong, H.P. King, J.P.C. (2011). Sensitivity of gust responses of bridges to spatio-temporal varying wind excitations, Canadian Journal of Civil Engineering, 2011, Vol. 38, No. 9 : pp. 963-973.

Hua, X. G., Chen, Z. Q., Ni, Y. Q., and Ko, J. M. (2007). Flutter analysis of long-span bridges using ANSYS. Wind and Structures, 10(1), 61-82.

Kaimal, J. C., Wyngaard, J. C., Izumi, Y., and Cote, O. R. (1972). Spectral characteristics of surface-layer turbulence. J. R. Met. Soc., 98(417), 563-589.

Lopez-Lopez, A., Perez-Rocha, L. E., Muñoz-Black, C. J., and Cordero-Macias, C. (2008). Wind velocities maps for Mexico using optimum design criterion. Reliability and Optimization of Structural Systems, Toluca, Mexico.

MOC (1993). Manual de diseño de obras civiles. Diseño por sismo, Instituto de Investigaciones Eléctricas, Comisión Federal de Electricidad (in Spanish).

MOC (2008). Manual de diseño de obras civiles. Diseño por sismo. Recomendaciones y comentarios, Instituto de Investigaciones Eléctricas, Comisión Federal de Electricidad.

NTCS (2004). Normas técnicas complementarias para diseño por sismo. Reglamento de Construcciones para el Distrito Federal, Gaceta Oficial del Departamento del Distrito Federal (in Spanish).

Rascón, O. A. (1999). Modelo de cargas vivas vehiculares para diseño estructural de puentes en México. Instituto Mexicano del Transporte y Secretaria de Comunicaciones y Transportes, publicación técnica No. 118, Sanfandila, Qro.

Scanlan, R. H., and Jones, N. P. (1990). Aeroelastic analysis of cable-stayed bridges. J. Struct. Eng, ASCE, 116(2), 229-297.

SCT (2001). Nueva normatividad para diseño de puentes. Pagina electrónica del IMT y la SCT, http://normas.imt.mx/default.htm, N-PRY-CAR-6-01-001/01 a N-PRY-CAR-6-01-006/01, Secretaria de Comunicaciones y Transportes.

Simiu, E., and Scanlan, R. H. (1996). Wind effects on structures, fundamentals and application to design. New York, John Wiley.

Fecha de publicación: 24 de febrero de 2025.